|
|
 |
|
 |
Navigation: Contents: Info: THE
K-MECHANISM It was Eddington who
theorised what he called the 'valve mechanism', that is if a
layer within the star became more opaque as it gets
compressed it would hold back a larger amount of heat trying
to get up to the surface. This would in effect make the star
expand. However as the star expands, the layer becomes more
transparent and heat would escape lowering the temperature
and so allowing the star to fall back in to start another
cycle. The level of opacity
of a layer must increase with compression, but Kramers law
that governs opacity says that in most regions of stars,
opacity actually decreases with compression. Kramers
Law:- The opacity The special conditions
where Eddingtons 'valve mechanism' can operate were
discovered some time later by a Russian astronomer
S.Zhevakin. The region inside a star called the partial
ionisation
zone create more ionised particles when they are compressed
rather than raise the temperature. When this happens, the
density increases more than the temperature and so the
opacity increases. This in term traps the heat and starts
the stars expansion. Now during the expansion, the
temperature does not drop by as much as what would be
expected because the ions recombine with the electrons
producing energy as they do so. The density also decreases
which in turn lowers the opacity and so allows the star to
contract and start the cycle again. Diagram showing the
opacity peak. The y-axis is the logarithm of the opacity,
the x and z-axis the logarithms of the temperature and
density respectively. The graph below shows the
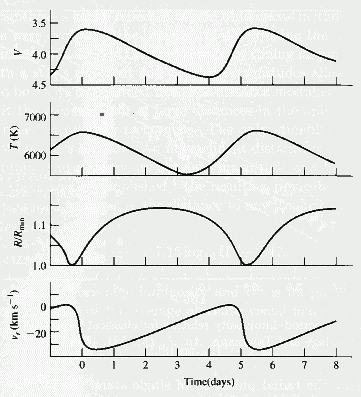
changing of magnitude of a Cepheid and its temperature.
Notice how the temperature (T) lags behind the magnitude
(V). Graph of Delta Cephei's
various parameters over a period of time
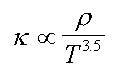
is both dependent on the stars density and temperature, but is more
dependent on the temperature due to its power of 3.5. This is why the
opacity usually increases upon compression, it takes special conditions
to overcome the damping effect of most stellar layers which explains
why pulsating stars are rare (around 1 in 
stars)
in the universe.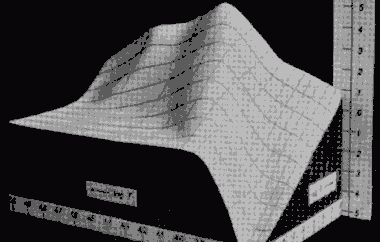
The
Radius Of Cepheid Variables
[ QUANTUMWEB SOFTWARE | QUANTUMWEB PUBLISHING ]